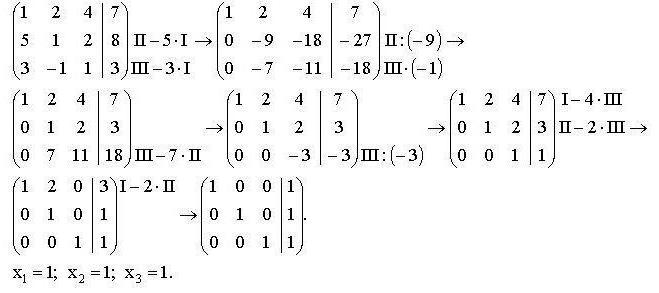שיטת איטרציה פשוטה לפתרון מערכות של משוואות לינאריות (SLAE)

שיטת איטרציה פשוטה, המכונה גם את השיטהקירוב רציף, הוא אלגוריתם מתמטי למציאת הערך של כמות לא ידועה על ידי זיקוק בהדרגה. המהות של שיטה זו היא, כפי שהשם מרמז, בהדרגה בפיתוח מן הקירוב הראשוני הבאים הבאים לקבל תוצאות מעודנות יותר ויותר. שיטה זו משמשת כדי למצוא את הערך של משתנה פונקציה מסוימת, כמו גם כדי לפתור מערכות של משוואות, הן ליניארי ולא ליניארי.

תן לנו לשקול כיצד שיטה זו מיושמת בפתרון SLAE. לשיטת האיטרציה הפשוטה יש את האלגוריתם הבא:

1. האימות של תנאי ההתכנסות במטריצה ​​הראשונית. משפט התכנסות: אם מטריצת המערכת המקורית היא באלכסון דומיננטי (כלומר, כל שורה של אלמנטים של האלכסון הראשי חייבת להיות גדולה בהיקפו מסכום אלכסוני צד הרכיבים בערך מוחלט), השיטה של ​​חזרות פשוטות - המתכנסת.

2. למטריצה ​​של המערכת המקורית לא תמיד יש דומיננטיות אלכסונית. במקרים כאלה, ניתן להמיר את המערכת. משוואות המספקות את מצב ההתכנסות נותרות ללא שינוי, ועם צירופים ליניאריים לא מספקים, למשל. להכפיל, להוסיף את המשוואות זה לזה עד לקבלת התוצאה הרצויה.

אם במערכת וכתוצאה מכך באלכסון הראשי ישנם מקדמים לא נוח, ולאחר מכן לשני חלקים של משוואה כזו להוסיף תנאים של הטופס ג_i* x_i, שעל סימניה להתמזג עם סימני האלמנטים האלכסוניים.

3. טרנספורמציה של המערכת המתקבלת לצורה הרגילה:

x^-49 β^-+ α * x^-

זה יכול להיעשות במספר דרכים, לדוגמה, כדלקמן: מן המשוואה הראשונה x Express₁ דרך אלמונים אחרים, מן השני₂, מן השלישי₃ וכן הלאה. אנו משתמשים בנוסחאות הבאות:

α_ij= - (א_ij / א_(ii)

_i= b_i/ א_ii
אנחנו חייבים שוב לוודא כי המערכת המתקבלת של צורה נורמלית תואמת את מצב ההתכנסות:

Σ (j = 1) | α_ij≤ 1, עם i = 1,2, ... n

4. אנו מתחילים ליישם, למעשה, את שיטת קירובים רצופים.

x⁽⁰⁾- קירוב ראשוני, אנו מבטאים את זה x⁽¹⁾, ולאחר מכן באמצעות x⁽¹⁾ x Express⁽²⁾. הנוסחה הכללית לתצוגת המטריצה ​​היא כדלקמן:

x⁽ⁿ⁾49 β^-+ α * x^(n-1)

אנו מחשבים עד שנגיע לדיוק הנדרש:

מקסימום x_i(k) -x_i(k + 1) ≤ ε

לכן, בואו לנתח בפועל את השיטה של ​​איטרציה פשוטה. דוגמה:
פתרון SLAE:

4.5x1-1.7x2 + 3.5x3 = 2
3.1x1 + 2.3x2-1.1x3 = 1
1.8x1 + 2.5x2 + 4.7x3 = 4 עם דיוק ε = 10^-3

הבה נראה אם ​​האלמנטים האלכסוניים ינצחו.

אנו רואים שרק המשוואה השלישית עונה על מצב ההתכנסות. אנו משנים את הראשון והשני, מוסיפים את השני למשוואה הראשונה:

7.6x1 + 0.6x2 + 2.4x3 = 3

מן השלישי אנו להפחית את הראשון:

-2.7x1 + 4.2x2 + 1.2x3 = 2

אנו המיר את המערכת המקורית לאחת מקבילה:

7.6x1 + 0.6x2 + 2.4x3 = 3
-2.7x1 + 4.2x2 + 1.2x3 = 2
1.8x1 + 2.5x2 + 4.7x3 = 4

עכשיו נביא את המערכת לצורה רגילה:

x1 = 0.3947-0.0789x2-0.3158x3
x2 = 0.4762 + 0.6429x1-0.2857x3
x3 = 0.8511-0.383x1-0.5319x2

בדוק את ההתכנסות של התהליך האיטרטיבי:

0.0789 + 0.3158 = 0.3947 ≤ 1
0.6429 + 0.2857 = 0.9286 ≤ 1
0.383+ 0.5319 = 0.9149 ≤ 1, כלומר תנאי הוא נפגש.

0,3947
קירוב ראשוני x⁽⁰⁾ = 0.4762
0,8511

החלפת ערכים אלה במשוואה של הצורה הרגילה, אנו מקבלים את הערכים הבאים:

0,08835
x⁽¹⁾= 0.486793
0,446639

להחליף את הערכים החדשים, אנו מקבלים:

0,215243
x⁽²⁾= 0,405396
0,558336

אנו ממשיכים את החישובים עד שאנו מתקרבים לערכים המספקים את המצב הנתון.

0,18813

x⁽⁷⁾0,441091

0,544319

0,188002

x⁽⁸⁾ = 0.44164

0,544428

בדוק את נכונות התוצאות:

4.5 * 0.1880 -1.7 * 0.441 + 3.5 * 0.544 = 2,0003
3.1 * 0.1880 + 2.3 * 0.441-1.1x * 0.544 = 0.9987
1.8 * 0.1880 + 2.5 * 0.441 + 4.7 * 0.544 = 3.9977

התוצאות המתקבלות על ידי החלפת הערכים שנמצאו במשוואות המקוריות מספקות את תנאי המשוואה.

כפי שאנו רואים, את שיטת איטרציה פשוטה נותן תוצאות מדויקות למדי, אבל כדי לפתור את המשוואה היינו צריכים לבלות הרבה זמן לעשות חישובים מסורבל.